Usage

Abstract tree classes

        graph TD;
Tree[Tree];
MutableTree[MutableTree];
DownTree[DownTree];
Tree[Tree];
MutableTree[MutableTree];
MutableDownTree[MutableDownTree];
MutableTree[MutableTree];
BinaryDownTree[BinaryDownTree];
BinaryTree[BinaryTree];
Tree-->MutableTree;
DownTree-->Tree;
DownTree-->MutableDownTree;
MutableDownTree-->MutableTree;
DownTree-->BinaryDownTree;
BinaryDownTree-->BinaryTree;
Tree-->BinaryTree;
    

A Downtrees is an object that has links to its direct children. A Tree is has links to both its children and its parent. A binary tree has exactly two children (left and right). A mutable tree can change its structure once created.

ABC	Inherits from	Abstract Methods	Mixin Methods
AbstractTree			nid, eqv()
DownTree	AbstractTree	children	nodes, descendants, leaves, levels, is_leaf, transform()
Tree	DownTree		siblings
MutableDownTree	DownTree	add_child(), remove_child()	add_children()
MutableTree	Tree, MutableDownTree		detach()
BinaryDownTree	DownTree	left_child, right_child	children
BinaryTree	BinaryDownTree, Tree

In your own code, you can inherit from these trees. For example, if your tree only has links to children:

import abstracttree
from abstracttree import print_tree

class MyTree(abstracttree.DownTree):
    def __init__(self, value, children=()):
        self.value = value
        self._children = children

    def __str__(self):
        return "MyTree " + str(self.value)

    @property
    def children(self):
        return self._children

You can now use this class in the following way to generate output:

tree = MyTree(1, children=[MyTree(2), MyTree(3)])
print_tree(tree)

# MyTree 1
# ├─ MyTree 2
# └─ MyTree 3

Adapter

In practice, not all existing tree data structures implement one of the abstract classes specified in Abstract classes. As a bridge, you can use Tree.convert to convert these trees to a Tree instance. However, whenever possible, it’s recommended to inherit from Tree directly for minimal overhead.

Tree.convert already does the right thing on many objects of the standard library:

# Inheritance hierarchy
Tree.convert(int)

# Abstract syntax tree
Tree.convert(ast.parse("1 + 1 == 2"))

# Filesystem
Tree.convert(pathlib.Path("abstracttree"))

# Zipfile
Tree.convert(zipfile.ZipFile("eclipse.jar"))

# Nested list
Tree.convert([[1, 2, 3], [4, 5, 6]])

It can also construct a tree by ducktyping on parent and children attributes:

# Works on objects by anytree, bigtree and littletree
Tree.convert(anytree.Node('node'))

Alternatively, you can use astree and explicitly specify how to find children and parent:

# Tree from json-data
data = {"name": "a",
        "children": [
            {"name": "b", "children": []},
            {"name": "c", "children": []}
]}
astree(data, children=operator.itemgetter["children"])

# pyqt.QtWidget
astree(widget, children=lambda w: w.children(), parent = lambda w: w.parent())

# Tree from treelib
astree(tree.root, children=lambda nid: tree.children(nid), parent=lambda nid: tree.parent(nid))

# itertree
astree(tree, children=iter, parent=lambda t: t.parent)

# Infinite binary tree
inf_binary = astree(0, children=lambda n: (2*n + 1, 2*n + 2))

Traversal

There are 3 common ways to traverse a tree:

Pre-order

The parent is iterated over before its children.

Post-order

The children are iterated over before their parent.

Level-order

Nodes closer to root are iterated over before nodes further from the root.

All these are possible by writing one of:

for node, item in tree.nodes.preorder():
    ...

for node, item in tree.nodes.postorder():
    ...

for node, item in tree.nodes.levelorder():
    ...

These methods return an item in addition to a node. This item is a tuple of the following fields:

depth

This indicates how deep the node is relative to the root of the (sub)tree iterated over. The root of the (sub)tree always has depth 0. To find the absolute depth of a node, use node.ancestors.count().

index

The index of this node among its siblings in relation to its direct parent. The first child of a parent gets index 0, the second gets index 1. The root of the (sub)tree always gets an index of 0 even if it has prior siblings.

To iterate over the descendants (the nodes without the root), similar methods are defined:

for descendant, item in tree.descendants.preorder():
    ...

If the order of iteration doesn’t matter an alternative way to iterate is as follows:

for node in tree.nodes:
    ...

for descendant in tree.descendants:
    ...

Export

Pretty printing:

print_tree(Path())
# .
# ├─ abstracttree
# │  ├─ abstracttree\conversions.py
# │  ├─ abstracttree\export.py
# │  ├─ abstracttree\predicates.py
# │  ├─ abstracttree\treeclasses.py
# │  └─ abstracttree\__init__.py
# ├─ LICENSE
# ├─ Makefile
# ├─ manual.txt
# ├─ pyproject.toml
# ├─ README.md
# └─ tests
#    ├─ tests\test_downtree.py
#    ├─ tests\test_export.py
#    ├─ tests\test_mutabletree.py
#    ├─ tests\test_tree.py
#    ├─ tests\test_uptree.py
#    └─ tests\tree_instances.py

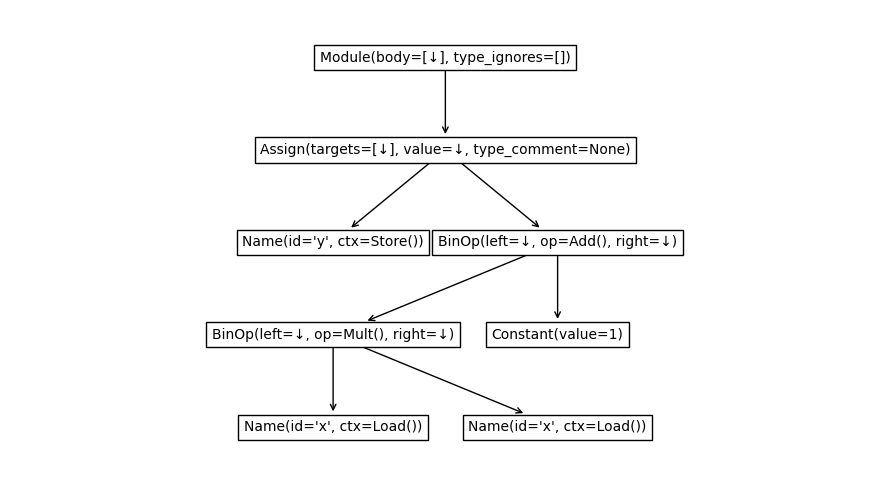
Plotting with matplotlib:

import matplotlib.pyplot as plt

plot_tree(ast.parse("y = x*x + 1"))
plt.show()

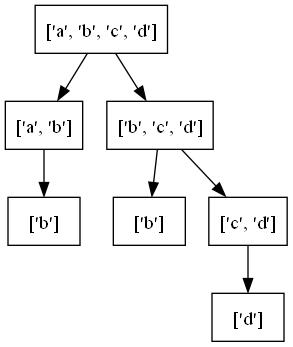
Export to graphviz:

tree = astree(seq, children=lambda x: [x[:-2], x[1:]] if x else [])
to_graphviz(tree)

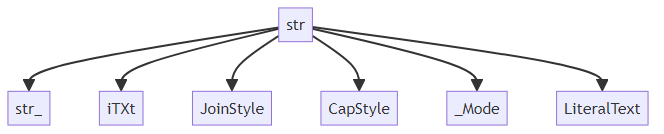
Export to mermaid:

to_mermaid(str)

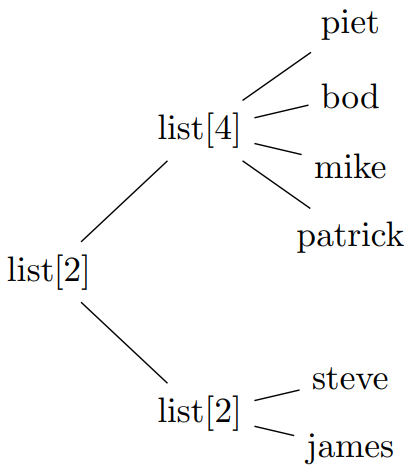
Export to latex:

data = [["james", "steve"],
        ["patrick", "mike", "bod", "piet"]]
to_latex(data)